(サムネイル画像:Gerd AltmannによるPixabayからの画像)
今回は Mathematica において関数を自作する方法を紹介します。
(2021年9月時点)
数学的な関数とプログラム的な関数
関数といっても、数学でいうところの関数とプログラミングでいうところの関数の両方が Mathematica では扱えるので、少し区別して考える必要があります。
それぞれに自作関数の作り方があるので、オイラー法によるロジスティック方程式の数値解析を通して1つずつ見ていきましょう。
数学的な関数を定義する
まずは数学的な関数を自作していきましょう。
Mathematica では左辺に自分のつけたい関数の名前、右辺に定義したい数式をおき、両者を := でつなぐことで数学的な関数を定義できます。
例えば、ロジスティック方程式は以下の常微分方程式で表されます。
$$ \frac{dx}{dt} = r x \left( 1 – \frac{x}{k} \right) $$
x は変数、r , k は定数です。
この右辺を Mathematica で関数 Function1 として定義してみます。

ここで、関数名の後ろについている [ ] 内には右辺に登場する文字(変数 x や定数 r , k)をアンダーバー付きで記す必要があります。
右辺の変数が緑色の斜体になっていればOKです。
これで Function1 と入力するとこの関数を呼び出せ、[ ] 内に代入したい値を入力すると計算結果を返してくれるようになりました。

以下も参照して下さい。
関数定義 | Wolfram言語プログラミングの基本
プログラミング的な関数を自作する
次にプログラミング的な関数を作るには、Mathematica の組み込み関数 Module を使います。
数学的な関数を定義したときと同様に、左辺に 関数名[変数1_,変数2_,・・・] を準備し、その後ろに :=Module[{・・・},・・・] と続けます。(・・・にはそれぞれ適切な表現が必要です。このまま入力しても動きません。)
{ } の中には作りたい関数の中に登場する変数(今回は x1)をすべて宣言しておく必要があります。
{ }, の後ろには関数として実行させたい処理を記述していきます。
以下のオイラー法の例では処理が1行しかありませんが、; を用いることで複数の処理を関数としてまとめることができます。

ここで、delta は Δt の代用であり、オイラー法における刻み幅を表します。
また、関数 EularLogistic の内部に 自作関数である Function1 を使っているので、EularLogistic を実行する前に必ず Function1 も実行しておきましょう。
これで r=1,k=20のとき、x=10の時点から時刻tを0.1だけ進めた先のxの値は10.5であることがわかりました。
しかし、これだけでは delta が1つ先の値が分かるだけなので、For文やリスト(配列)と組み合わせてオイラー法を実行しましょう。

これで r=1,k=20 のロジスティック方程式において、初期値 x[0]=1 としたときの t=0 から t=1 まで 0.1 刻みの x[t] の値を出力することができました。
Module に関する詳細は以下を確認してください。
Module—Wolfram言語ドキュメント
おまけ1: 数値計算の結果をグラフ化する
先程計算したロジスティック方程式の数値計算結果をグラフ化してみましょう。
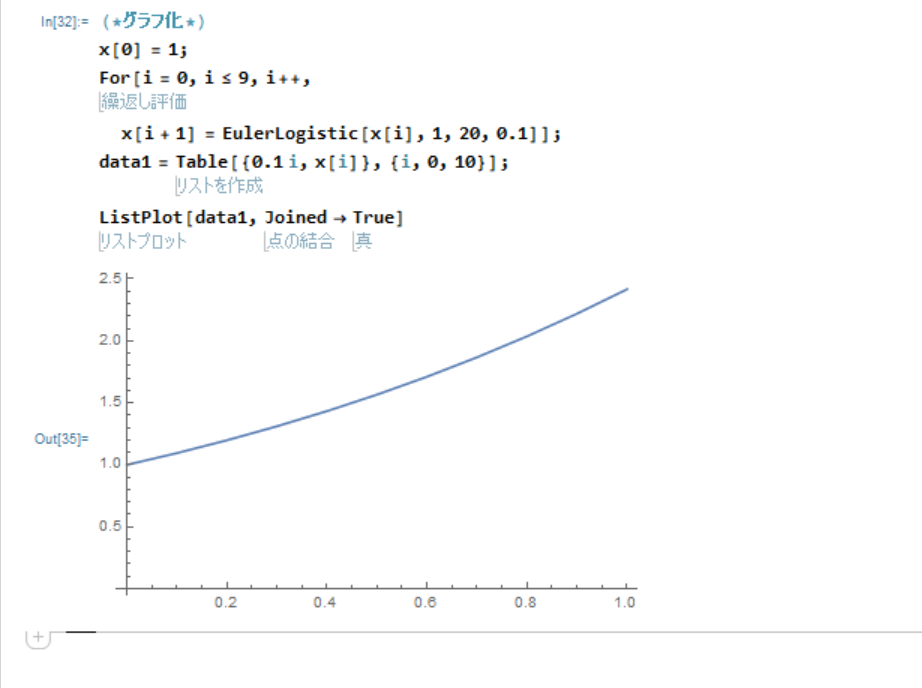
ここで、Table というリスト作成の組み込み関数や ListPlot というグラフ化の組み込み関数を用いていますが、これらの使い方については以下を参照して下さい。
おまけ2:数値計算からグラフ化までをさらに関数化する
先程作った関数 EularLogistic を改良すれば、数値計算からグラフ化までの処理も1つの関数にまとめることができます。
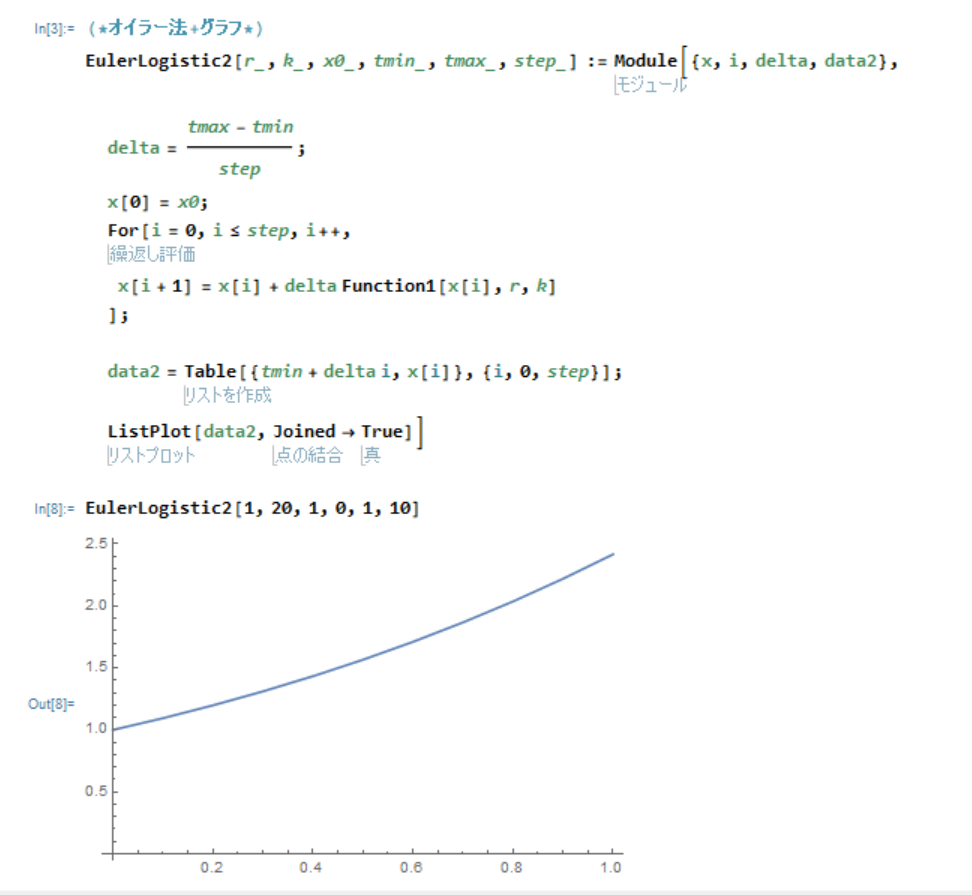
ここでは時刻 t の最小値 tmin と最大値 tmax を設定することができるようにしており、x0 は初期値、つまり x[tmin]=x0 となります。
それに伴い、刻み幅 delta ではなく時刻 t の分割回数(オイラー法におけるステップ数) step を入力としています。
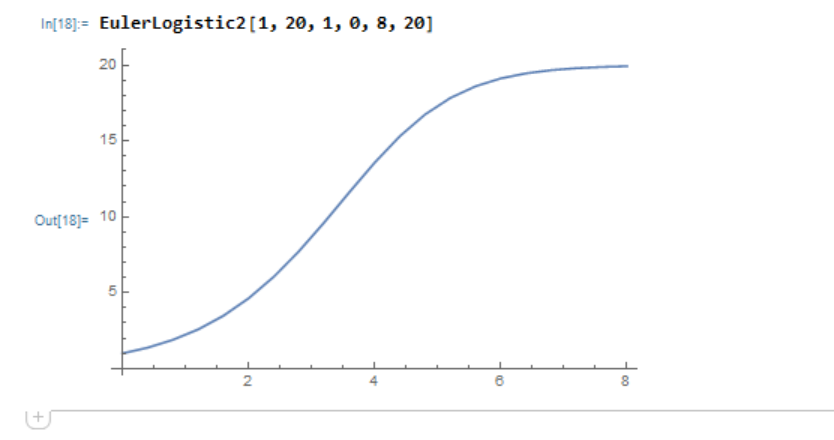
ちなみに tmax や step を増加させるなど、もう少し計算量を増やせばロジスティック方程式の特徴的なシグモイド曲線が表れます。
まとめ
今回は Mathematica で数学的な関数とプログラミング的な関数を作る方法、簡単な数値計算とグラフ化の方法を紹介しました。
これでよく使う処理を何度もコピペしなくても楽に使えるようになったと思います。
関数化やオイラー法、グラフ化に関しては、紹介した方法よりもスマートな方法もあると思うので、是非使いやすいように改良してみて下さい。