(サムネイル画像:MediamodifierによるPixabayからの画像)
今回は Mathematica でグラフを作成する方法、そしてグラフ作成時に便利なオプション関数について紹介します。
(2022年3月時点)
グラフの描き方
y=f(x) のグラフ
まずは基本となるグラフを描いてみましょう。
y=f(x) の形で表すことができるグラフであれば、Plot 関数を用いて描くことができます。
今回は例として3次関数
$$ y =x^3-x^2-10x $$
を描いてみます。
次のように入力しましょう。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}]Plot 関数の中には y=f(x) の f(x) 部分だけを入力します(「y=」は不要です)。
, の後の中括弧 { } には横軸にしたい変数を宣言し(今回は x)、その定義域(今回は -5 から 5 まで)を設定します。
実行すると、
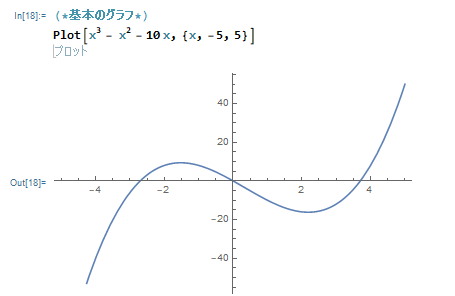
このようにグラフが描けました。
Plot 関数に関して、詳細は以下をご覧ください。
直線のグラフ
直線のグラフの場合、横線のグラフは Plot 関数で描くことができます。
なぜなら y=(定数) とするだけだからです。
Plot[3, {x, -5, 5}]これを実行すると、
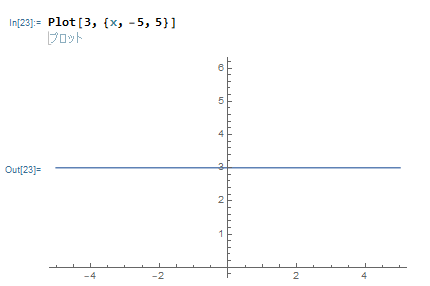
このように描けます。
しかし、縦線は x=(定数) となるので、Plot 関数では描けません。
そこで使うのが ParametricPlot 関数です。
ParametricPlot 関数は [{f(u),g(u)},{u,u_min,u_max}] という引数を用いて、本来は x 座標が f(t)、y 座標が g(t) であるようなグラフを描く関数です。
ParametricPlot[{Sin[u],Sin[2u]},{u,0,2 Pi}]として実行すると、
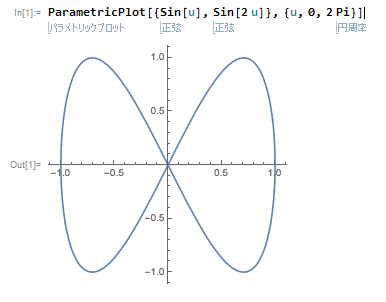
というグラフが描けます。
ここではこれを利用して、x=(定数) のグラフを描いてみます。
ParametricPlot[{{2, t}}, {t, -1, 1}]として実行すると、x=2 の縦線(高さ y は -1~1)のグラフが
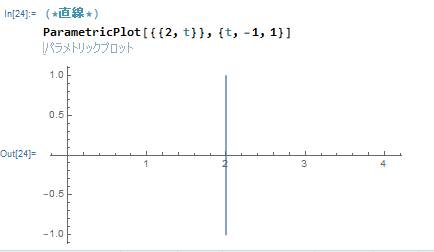
このように描けます。
ParametricPlot 関数に関して、詳細は以下をご覧ください。
微分方程式のグラフ
今回はロジステック方程式
$$ x'(t) = r x \left( 1 – \frac{x}{K} \right) $$
で、r=K=1 とした場合のグラフを描いてみます。
微分方程式のグラフを描かせるためには、DSolve や NDSolve 関数を用いて解を求める必要があり、その後、解をプロットします。
ここでは NDSolve を用いて、初期値 x(0)=0.1、時間 t は 0 から 10 までの解 sol を求めています。
sol = NDSolve[{x'[t] == x[t] (1 - x[t]), x[0] == 0.1}, x, {t, 0, 10}];
Plot[Evaluate[x[t] /. sol], {t, 0, 10}]これを実行すると、
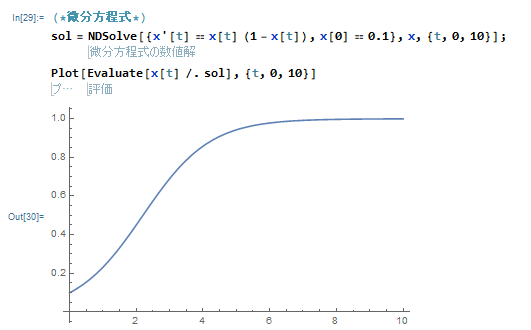
というグラフが描けます。
微分方程式のグラフで用いた関数についてはこちらを参照してください。
オプション関数
Mathematica のデフォルトのグラフは青線で描かれます。
デフォルトのままでも十分きれいですが、用途によっては「もっとこうしたい」という部分が出てくるでしょう。
ここからは、最初の3次関数のグラフをベースに様々なオプション関数を用いて改良していきます。
線を太くする、色を変える、破線にする
まずは、線を太くする、色を変える、破線にするといった操作をしてみましょう。
これらはすべて PlotStyle というオプション関数で行えます。
オプション関数とは、メインとなる関数(今回は Plot)の中で作用させる補助的な関数で、メイン関数の中に , に続けて入力します。
ここでは線を太くする、色を黒に変える、破線にするという3つの操作をしてみます。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> Thick]Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> Black]Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> Dashed]それぞれ実行すると、
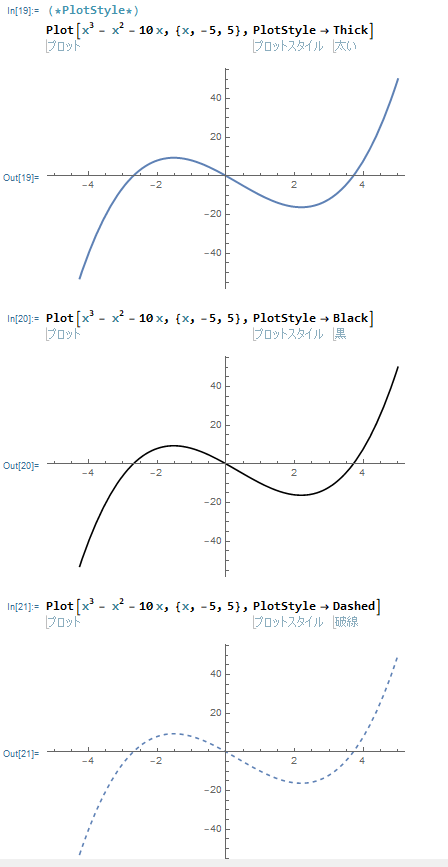
このようなグラフが描けました。
色は Black のところを Red や Green にすることで、好きに変えることができます(Blue はデフォルトのカラー)。
たいていの色はこれで指定できますが、さらに細かい色設定をしたい場合、RGBColor というオプション関数を使って、
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> RGBColor[1,0,1]]などとできます。
引数は [Red,Green,Blue] で、0~1 の値を入力します。
太さに関しても Thickness という関数でより細かく調整ができます。
また、これらは中括弧 { } で組み合わせることができ、
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> {RGBColor[1, 0, 1], Dashed, Thick}]とすると、
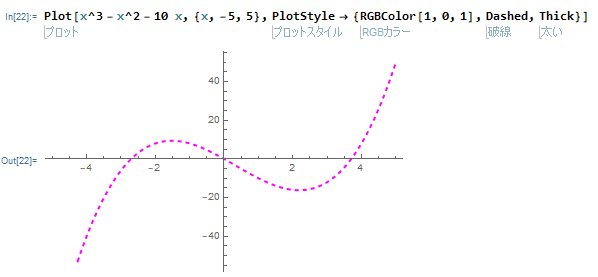
というグラフも描けます。
PlotStyle の中のオプション関数も RGBColor や Thickness 以外にもたくさんあるので、詳しくは以下を参考にしてください。
全体のサイズ、縦横比を変更する
グラフ全体のサイズを変更する場合は ImageSize 、縦横比を変更する場合は AspectRatio という関数を使います。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, ImageSize -> Small]Plot[x^3 - x^2 - 10 x, {x, -5, 5}, ImageSize -> Large ]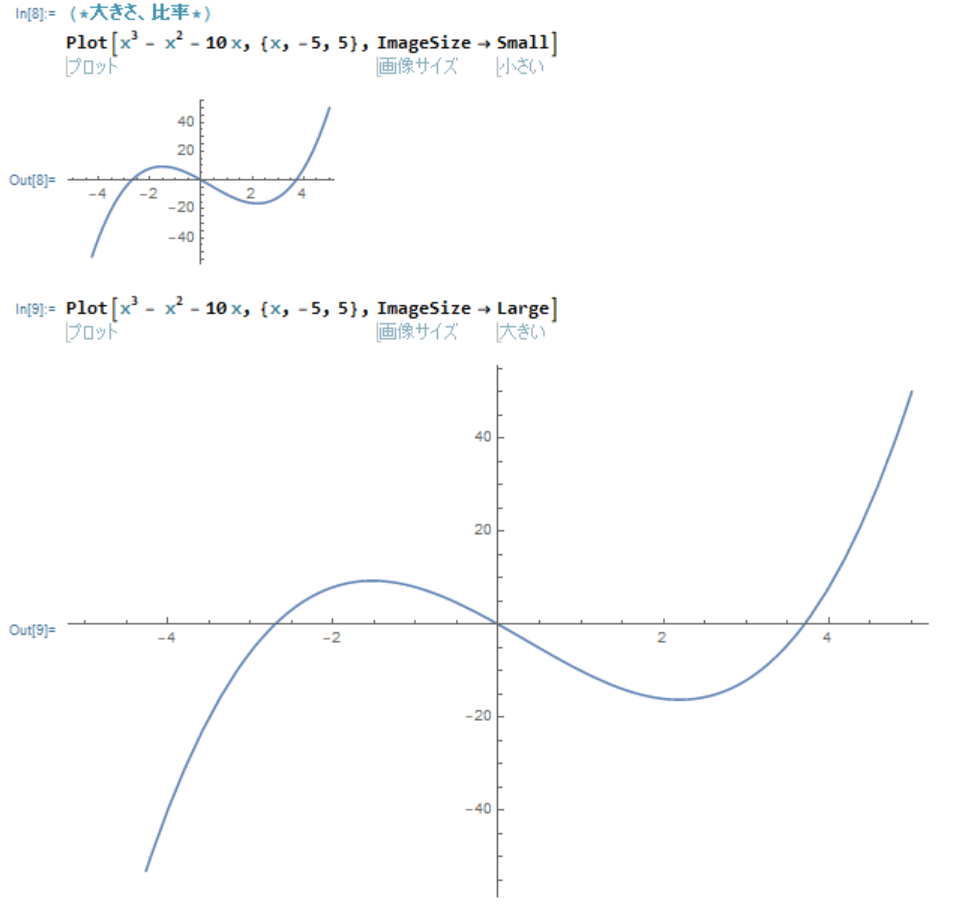
このように ImageSize では、Tiny, Small, Medium, Large, Full でサイズを指定できます。
デフォルトは Medium であることが多いです。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, AspectRatio -> 1/2]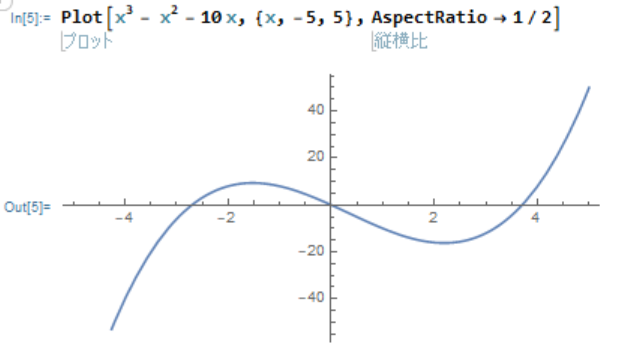
AspectRatio では縦横比を変更できます。
1/GoldenRatio とすれば、黄金比も利用できます。
(デフォルトが黄金比の場合もあります。)
軸
グラフの軸はデフォルトでも表記されていますが、少し物足りなさを感じるかと思います。
ここでは、使う機会の多そうな Axes, Ticks, AxesLabel, Style, LabelStyle というオプション関数を紹介します。
Axes では軸を、Ticks では軸の目盛りを書くかどうかを決められます。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> False]Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Ticks -> None]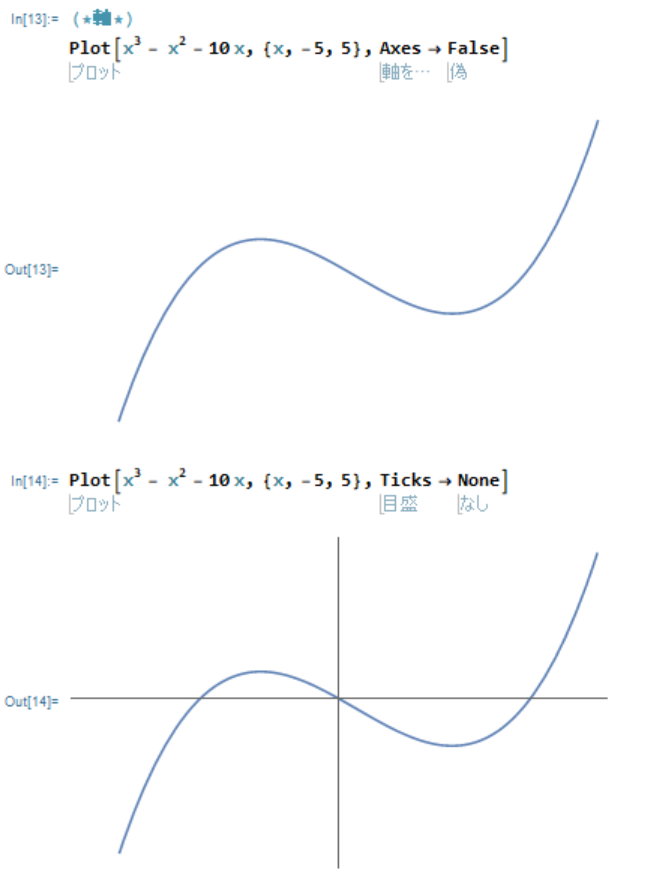
デフォルトではどちらも書く設定になっているので、グラフの概形だけわかればいい場合は None とすると消すことができます。
また、Axes に関しては x軸とy軸を別々に指示することもできるので、組み合わせると、
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True,False}, Ticks -> None]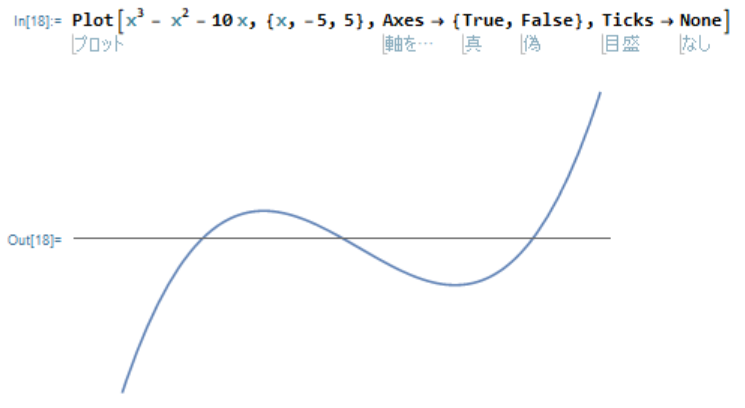
とすることもできます。
こうなるとx軸が分かりずらいので、軸の名前をつけましょう。
そのときに利用するのが、AxesLabel です。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True,False}, Ticks -> None, AxesLabel -> Automatic]Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True,False}, Ticks -> None, AxesLabel -> {"z"}]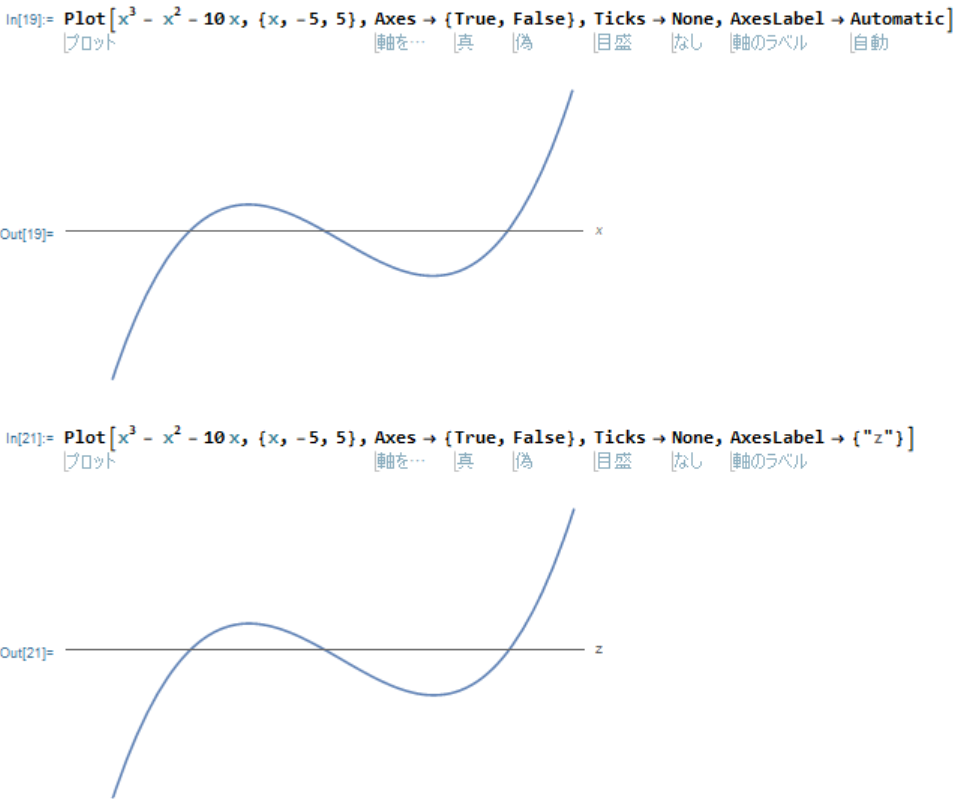
Automatic とすれば、自動で名前をつけてくれますが、自分で決めることもできます。
次に、交点の座標を記入してみましょう。
3次方程式
$$x^3-x^2-10x=0$$
の解は
$$x=0, x=\frac{1 \pm \sqrt{41}}{2}$$
ですが、今回はそれぞれの座標を x=a, 0, b として表示してみます。
これには先ほどの Ticks により複雑な入力をします。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True, False},
Ticks -> {{{(1 - Sqrt[41])/2, "a"}, 0, {(1 + Sqrt[41])/2, "b"}}},
AxesLabel -> Automatic]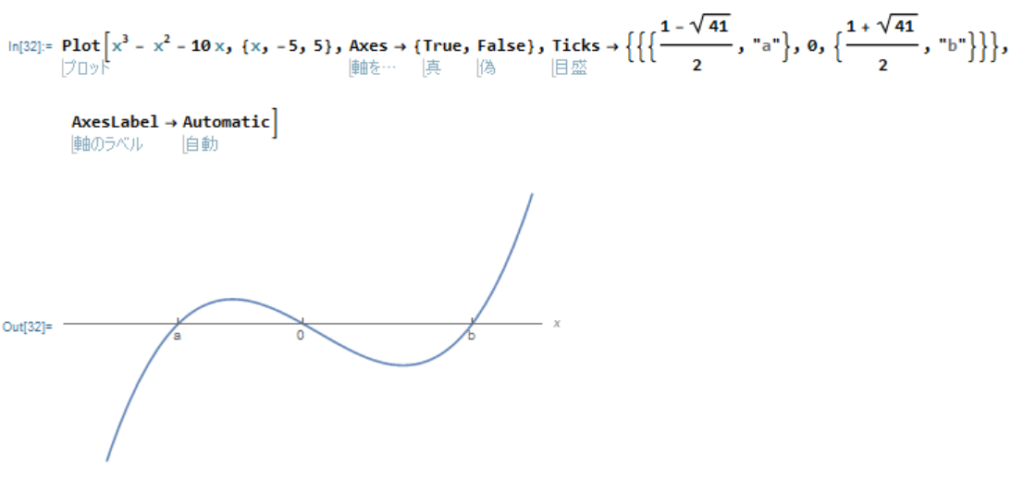
その数値の座標をそのまま記入することは比較的簡単ですが、文字に置き換えるとなると少し複雑になります。
最後に、グラフ中の文字のフォントやサイズの変更の仕方を紹介します。
先ほどのグラフで、軸の名前や交点の座標を斜体にするには、
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True, False},
Ticks -> {{{(1 - Sqrt[41])/2, Style["a", Italic]},
0, {(1 + Sqrt[41])/2, Style["b", Italic]}}},
AxesLabel -> {Style["x", Italic]}]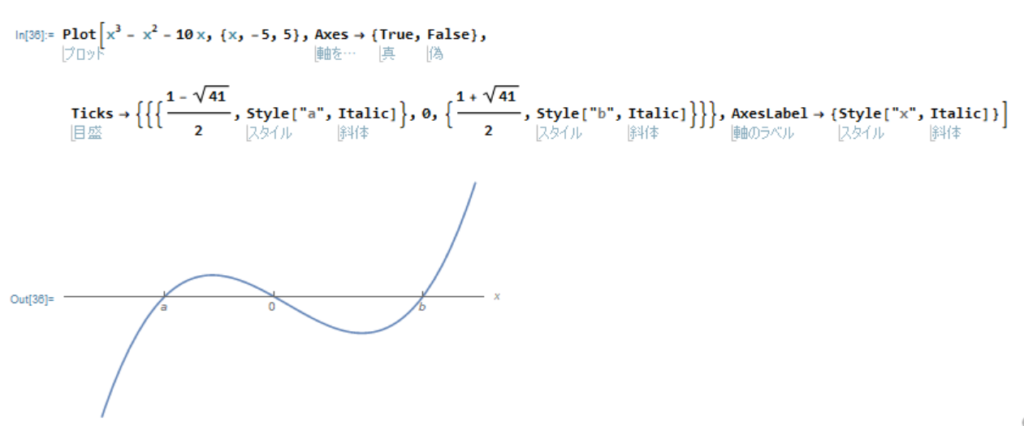
このように Style 関数で個別に設定することもできますが、LabelStyle というオプション関数を用いることで、グラフ中のすべての文字を斜体にしたり、太字にしたり、フォントや文字サイズを変えたりできます。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, Axes -> {True, False},
Ticks -> {{{(1 - Sqrt[41])/2, "a"}, 0, {(1 + Sqrt[41])/2, "b"}}},
AxesLabel -> {"x"},
LabelStyle -> {FontFamily -> "Times New Roman", 21, GrayLevel[0],
Bold, Italic}]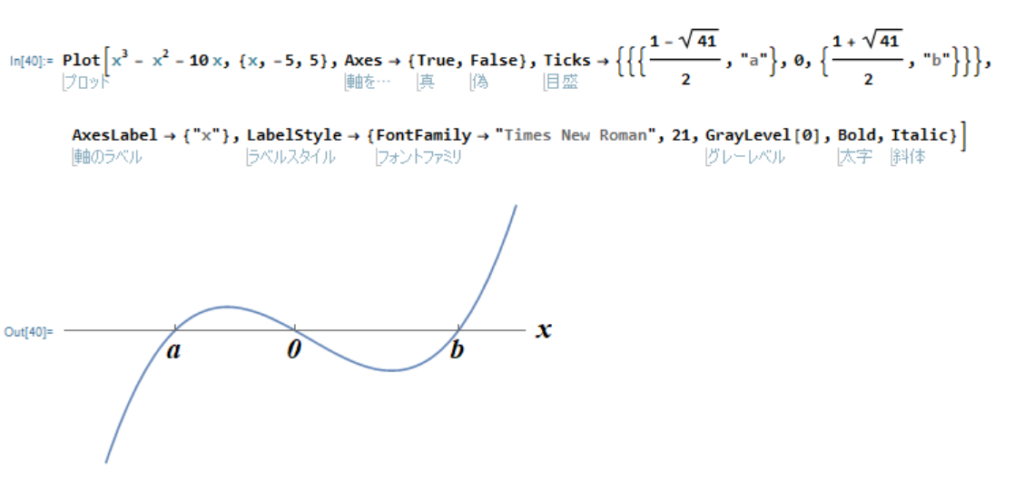
ここで使ったオプション関数について、詳しくは以下を参考にしてください。
その他
その他のオプション関数として、PlotRange と MaxRecursion を紹介します。
PlotRange はグラフの範囲を指定する関数です。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotRange -> {{0, 7}, {-3, 3}}]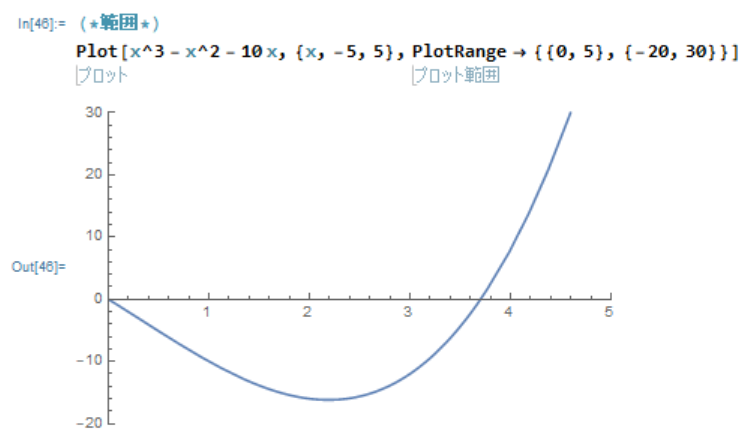
x座標とy座標を用いて範囲を制限します。
また、MaxRecursion は再帰分割の最大数を指定するオプション関数です。
再帰分割とは何だ?という感じですが、グラフを描くにあたっての演算回数といったイメージでいいと思います。
Plot[x^3 - x^2 - 10 x, {x, -5, 5}, MaxRecursion -> 5]デフォルトの値が小さいため、5にするだけでもグラフの質が上がります。
しかし、3次関数ぐらいでは全く恩恵を感じることはありません。
演算回数が必要な3Dグラフを描いたりや領域に色を塗ったりしたときに、グラフの表示が変な場合は試してみてください。
複数のグラフを組み合わせる
最後に、グラフを組み合わせて表示する方法などのを紹介します。
新たに使う関数は Show です。
例として、3次関数と縦線のグラフを同時に表示してみましょう。
3次関数のグラフを fig1、縦線のグラフを fig2 として、それらを Show で表示するだけです。
fig1 = Plot[x^3 - x^2 - 10 x, {x, -5, 5}, PlotStyle -> {Thick, Red}];
fig2 = ParametricPlot[{{2, t}}, {t, -50, 50}];
Show[fig1, fig2]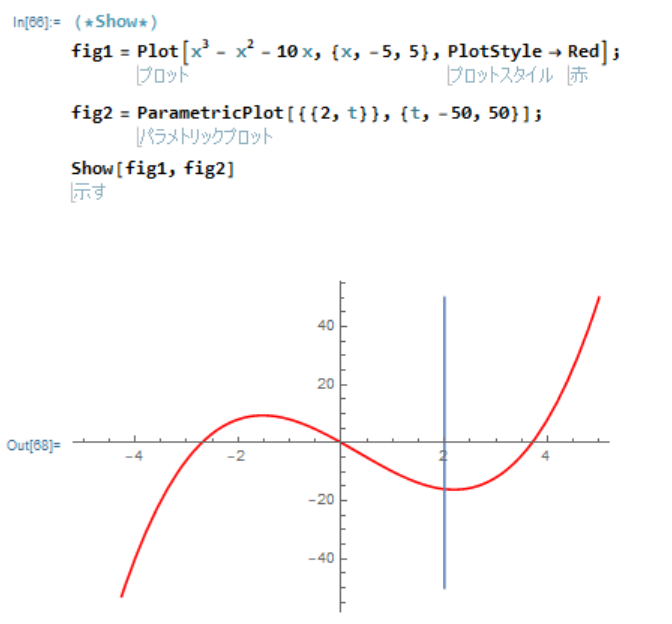
見やすくするため、fig1 は赤色にしてあります。
上で紹介した Plot のオプション関数は、Show 内でも使えるものが多いので、全体をまとめてサイズを調整したりもできます。
ここで使ったオプション関数について、詳しくは以下を参考にしてください。
まとめ
オプション関数をたくさん紹介しましたが、これらを使いこなせればかなり自由にグラフが描けるのではないでしょうか。
まだ触れていないオプション関数もたくさんあるので、是非色々な機能を活用してみてください。
参考
- AspectRatio—Wolfram言語ドキュメント
- Axes—Wolfram言語ドキュメント
- AxesLabel—Wolfram言語ドキュメント
- DSolve—Wolfram言語ドキュメント
- Evaluate—Wolfram言語ドキュメント
- ImageSize—Wolfram言語ドキュメント
- LabelStyle—Wolfram言語ドキュメント
- MaxRecursion—Wolfram言語ドキュメント
- NDSolve—Wolfram言語ドキュメント
- ParametricPlot—Wolfram言語ドキュメント
- Plot—Wolfram言語ドキュメント
- PlotRange—Wolfram言語ドキュメント
- PlotStyle—Wolfram言語ドキュメント
- Show—Wolfram言語ドキュメント
- Style—Wolfram言語ドキュメント
- Ticks—Wolfram言語ドキュメント





とてもありがたい